https://m.blog.naver.com/PostView.nhn?blogId=samsjang&logNo=221033626685&proxyReferer=https%3A%2F%2Fwww.google.co.kr%2F
아래 내용들은 위 링크 게시물에 추가적인 설명만 덧붙인 겁니다.

오차제곱합의 미분(본인)

Sigmoid 함수의 미분
출처 : http://taewan.kim/post/sigmoid_diff/



오차합의 가중치에 대한 미분 (본인 계산)
두번째 게시물의 링크와 내용입니다.
https://m.blog.naver.com/samsjang/221035217759
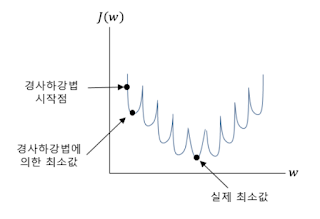
위 그림을 보면 우리가 첫번째 게시물에서 다뤘던 gradient descent 방법 만으로는 모든 경우에 대한 최소값을 구하기 어려운 것을 알 수 있다.
이를 해결하기 위해 로지스틱 회귀를 위한 비용함수를 만들게 된다.

경사하강법이 성공적으로 적용되려면 볼록형태의 그래프를 가진 함수이어야 하며, 위와 같은 수식을 이용하면 그래프가 볼록한 모양으로 되는 새로운 비용함수 그래프를 얻을 수 있다.


흠... 이거 아닌가?






댓글 없음:
댓글 쓰기